Conducting Sphere Bistatic Scattering
This example demonstrates the accuracy of XFdtd for scattering from a conducting sphere. The bistatic scattering pattern from an incident plane wave is computed at a single frequency.
The sphere is considered perfectly conducting and measures 254 mm in diameter. The sphere is centered at the origin and an incident plane wave arrives from the +X direction as shown in Figure 1. The far field bistatic RCS pattern is computed in a circular arc surrounding the sphere in the XY plane as shown by the red circle in Figure 1. The plane wave is shown as the yellow arrow at the right of the figure and the electric field is oriented along the Y axis. The input signal is a 10 GHz sinusoid.
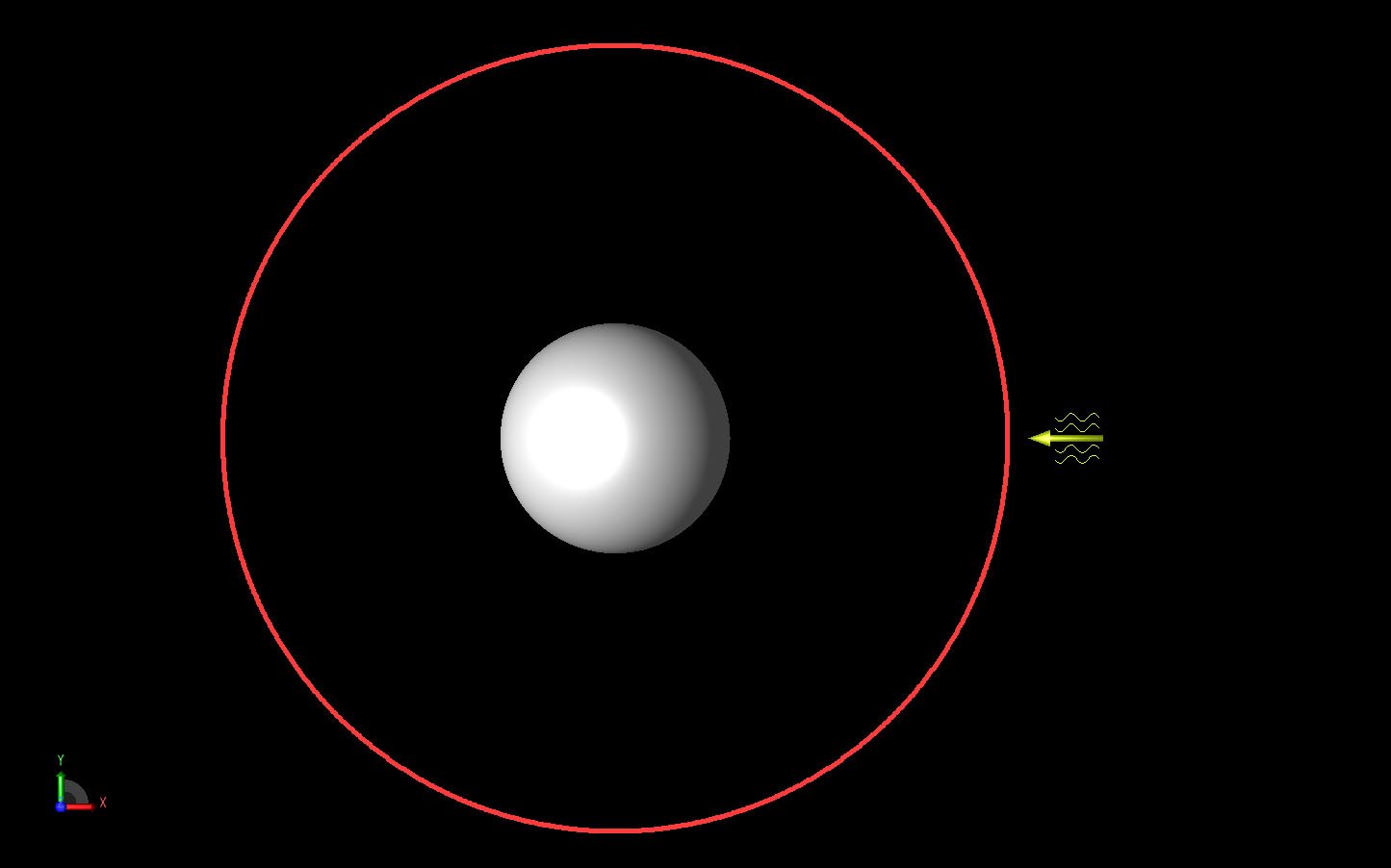
Figure 1: The sphere geometry is shown with the incident plane wave displayed as a yellow arrow to the right. The red circle represents the far field pattern that will be computed in the XY plane.
The sphere is meshed in an FDTD grid with a cell size of 1 mm which represents 30 cells per wavelength as shown in Figure 2. A separation of 20 FDTD cells surrounds the object which terminates in an outer boundary using seven perfectly match layers (PML) to absorb the fields. The project requires about 965 MB of memory to run.

Figure 2: The sphere shown meshed in the FDTD grid at a cell size of 1 mm.
The simulation is performed using the Scattered Field formulation in the software and run on an Intel Core i7-2640M CPU at 2.80 GHz. The simulation requires about 21 minutes to run. The resulting bistatic scattering pattern in the forward direction is compared to measured results from a published paper [1] and shows very good agreement as may be seen in Figure 3. The full bistatic pattern in shown as a polar plot around the XY in Figure 4. Three dimensional views of the bistatic pattern are shown in Figures 5, 6, and 7. In Figures 8 and 9 the transient electric field in the plane passing through the center of the sphere is displayed at two time instances. In Figure 8 the incident plane wave has struck the sphere but has not fully propagated around the surface. In Figure 9, the incident plane wave has fully engulfed the sphere and the steady-state field pattern is shown.
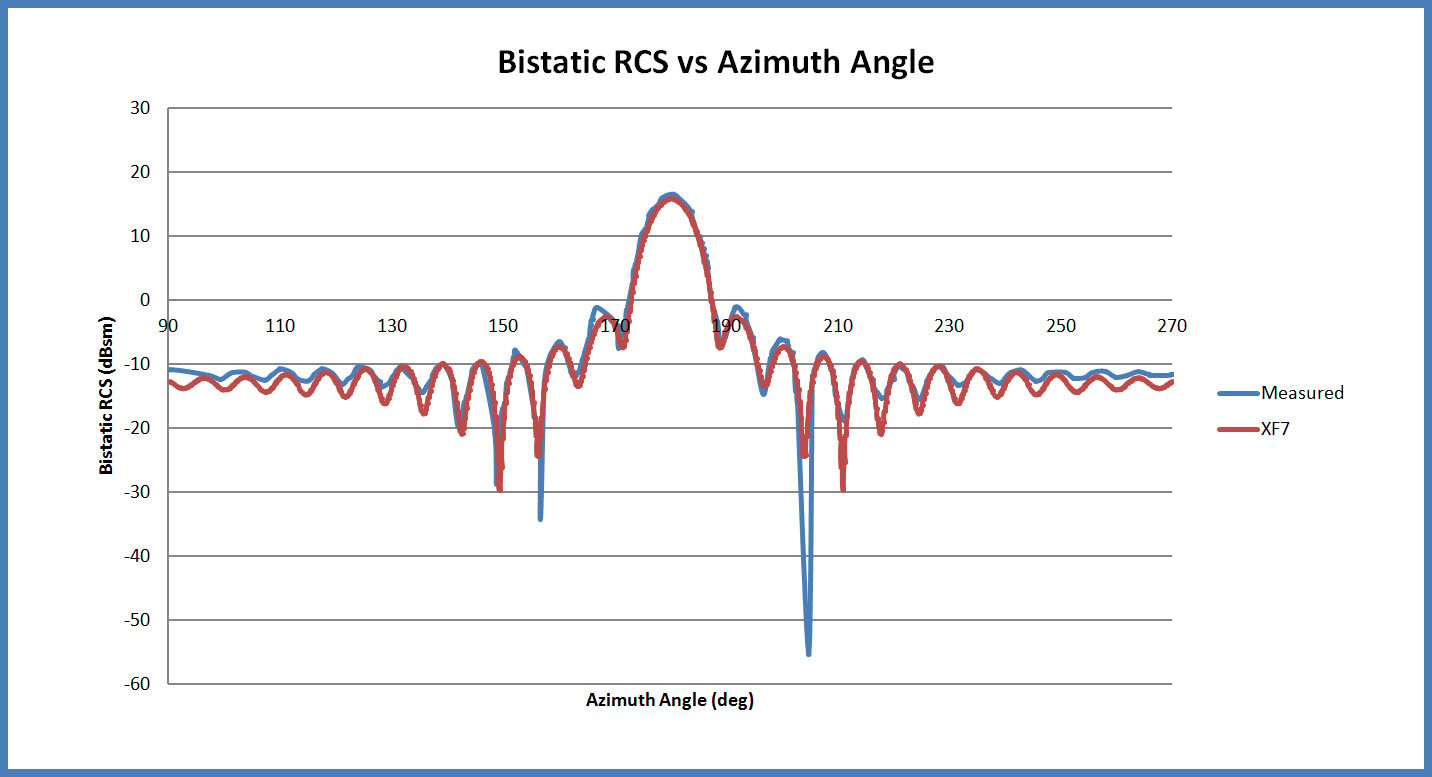
Figure 3: The computed bistatic radar cross section compared with measured results for the forward scatter direction. Excellent agreement is found.
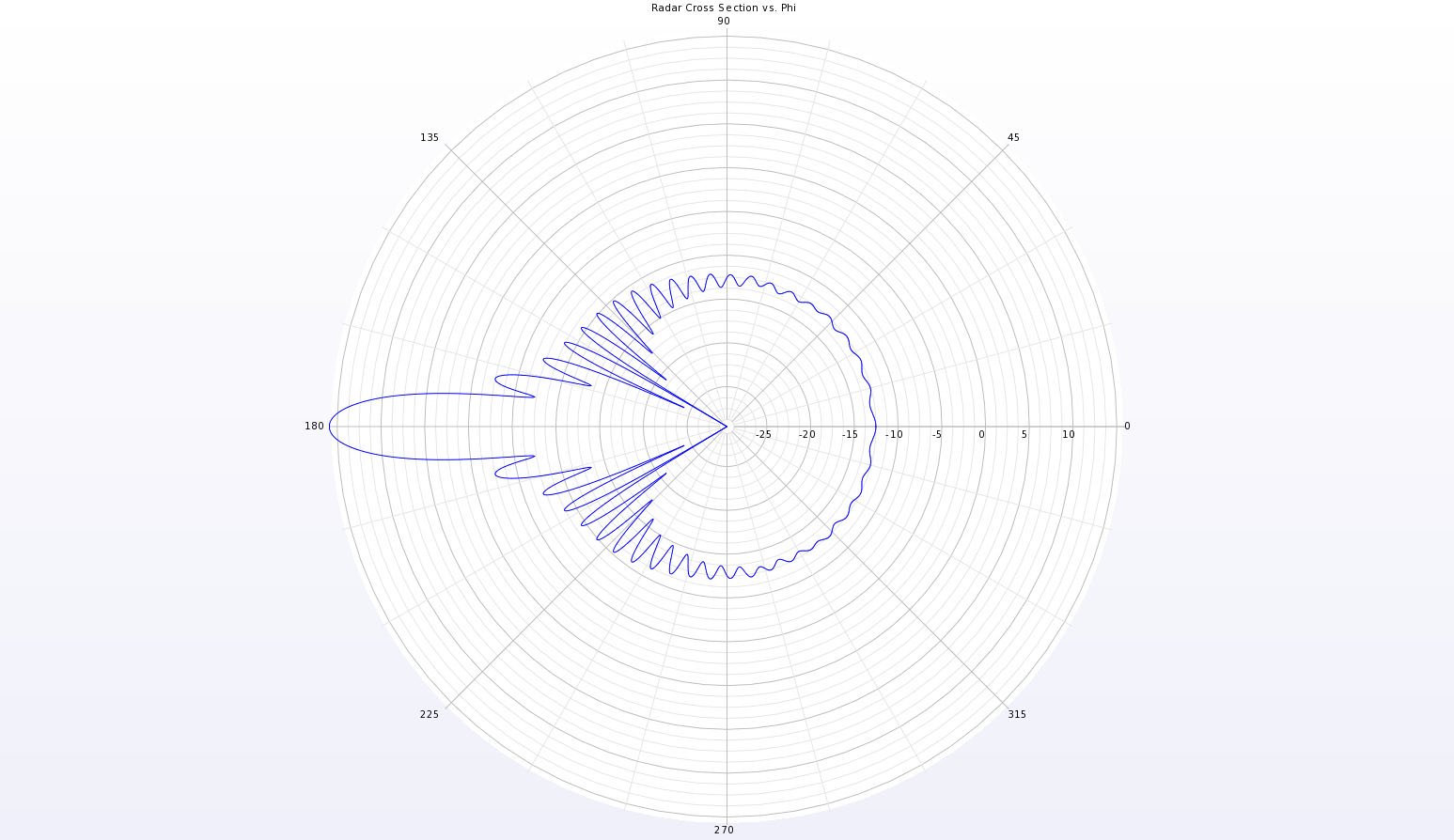
Figure 4: A full polar plot in the XY plane of the bistatic scattering pattern for the sphere.
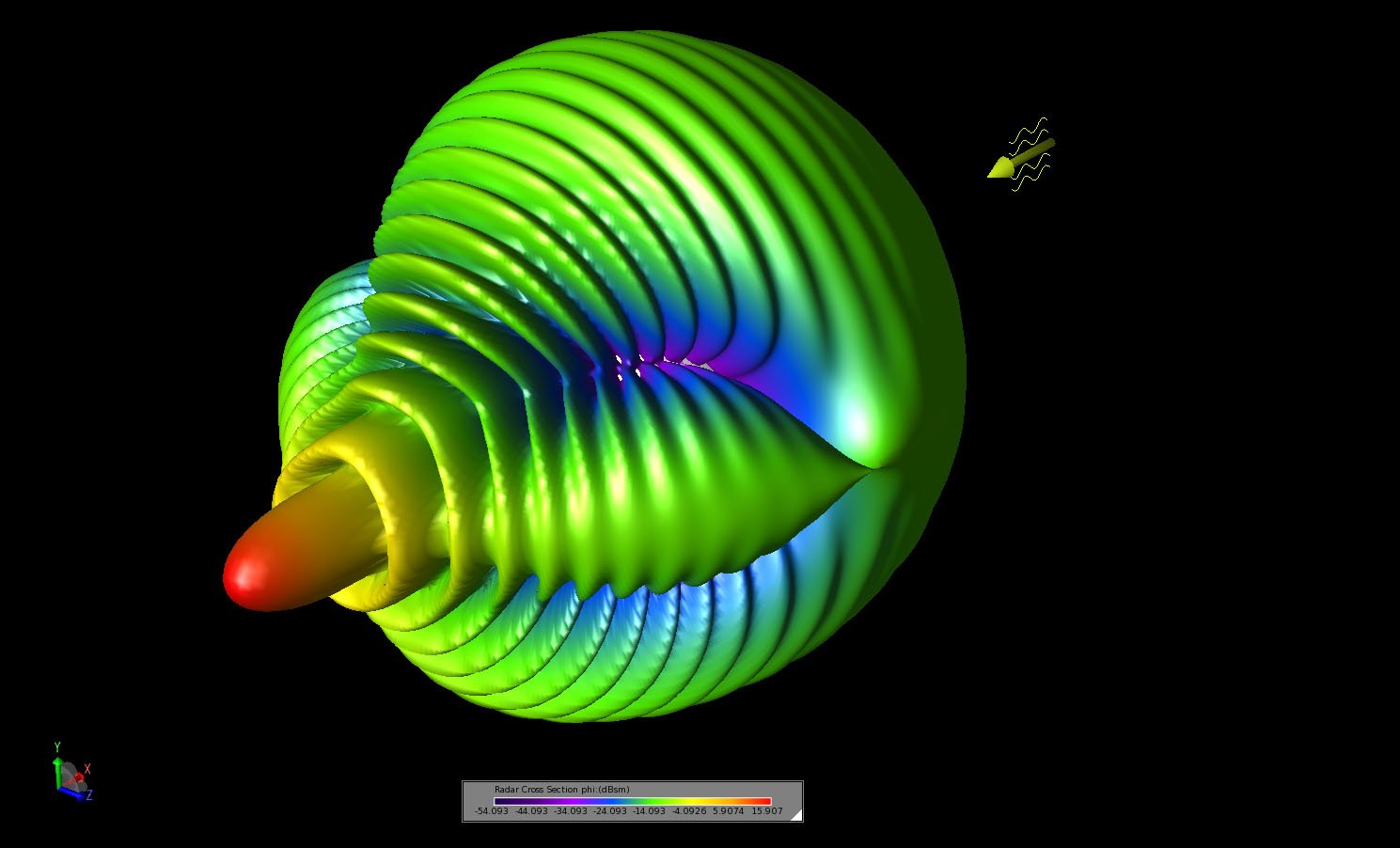
Figure 5: A three-dimensional view of the bistatic scattering pattern shown from an angled viewing position at the forward end of the pattern.
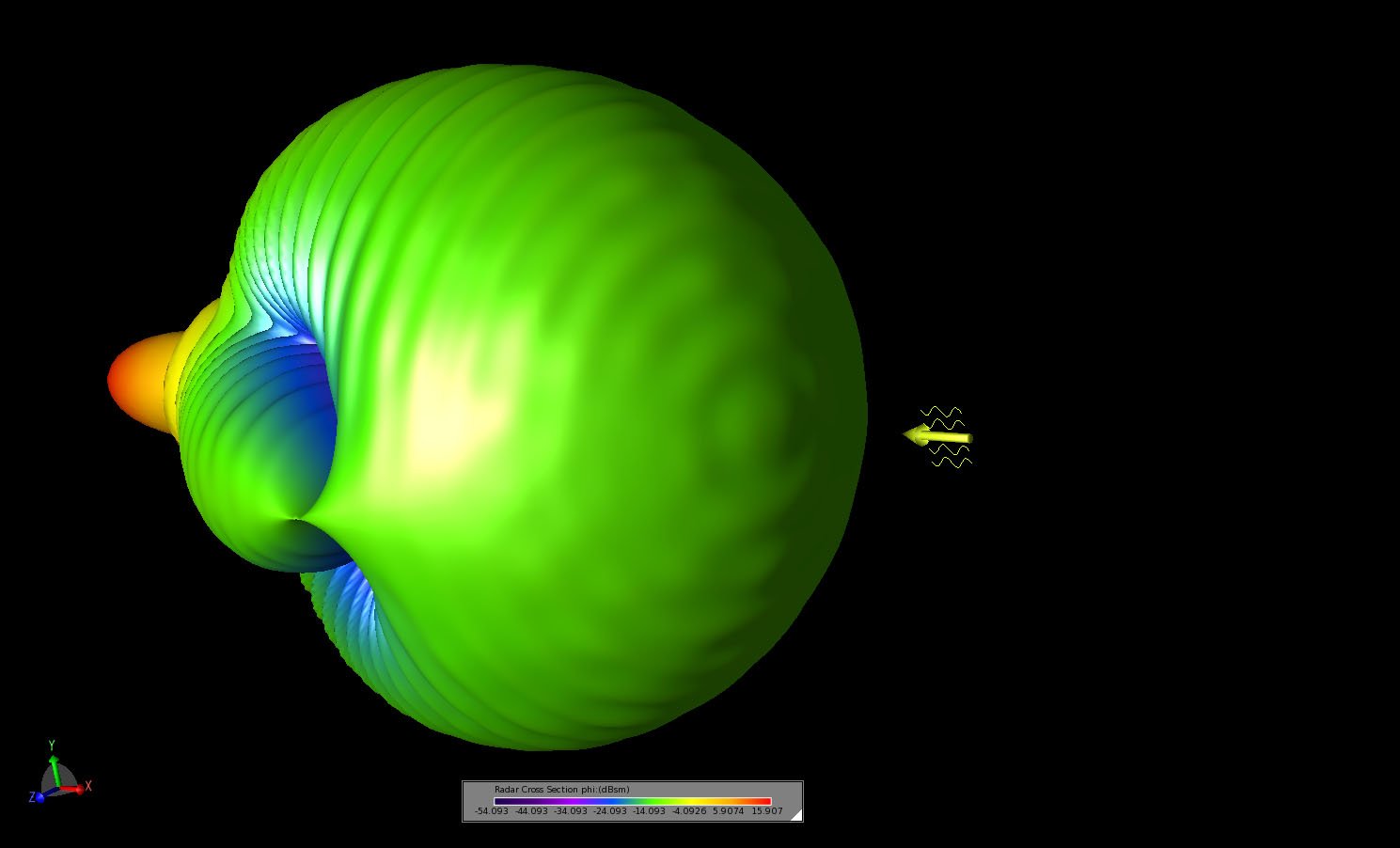
Figure 6: A three-dimensional view of the bistatic scattering pattern shown from an angled viewing position in the backscatter direction of the pattern.
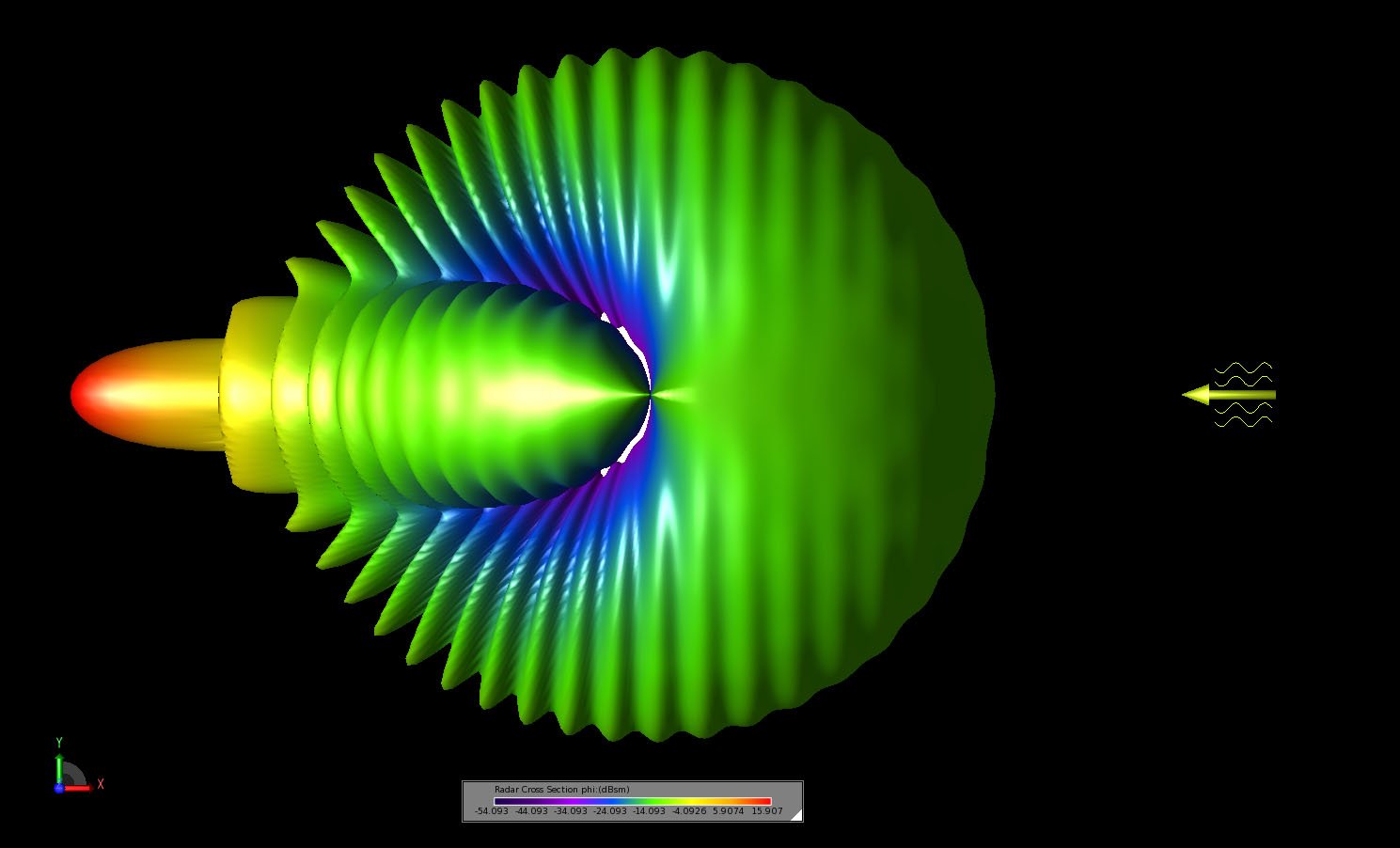
Figure 7: A three-dimensional view of the bistatic scattering pattern shown in the XY plane.
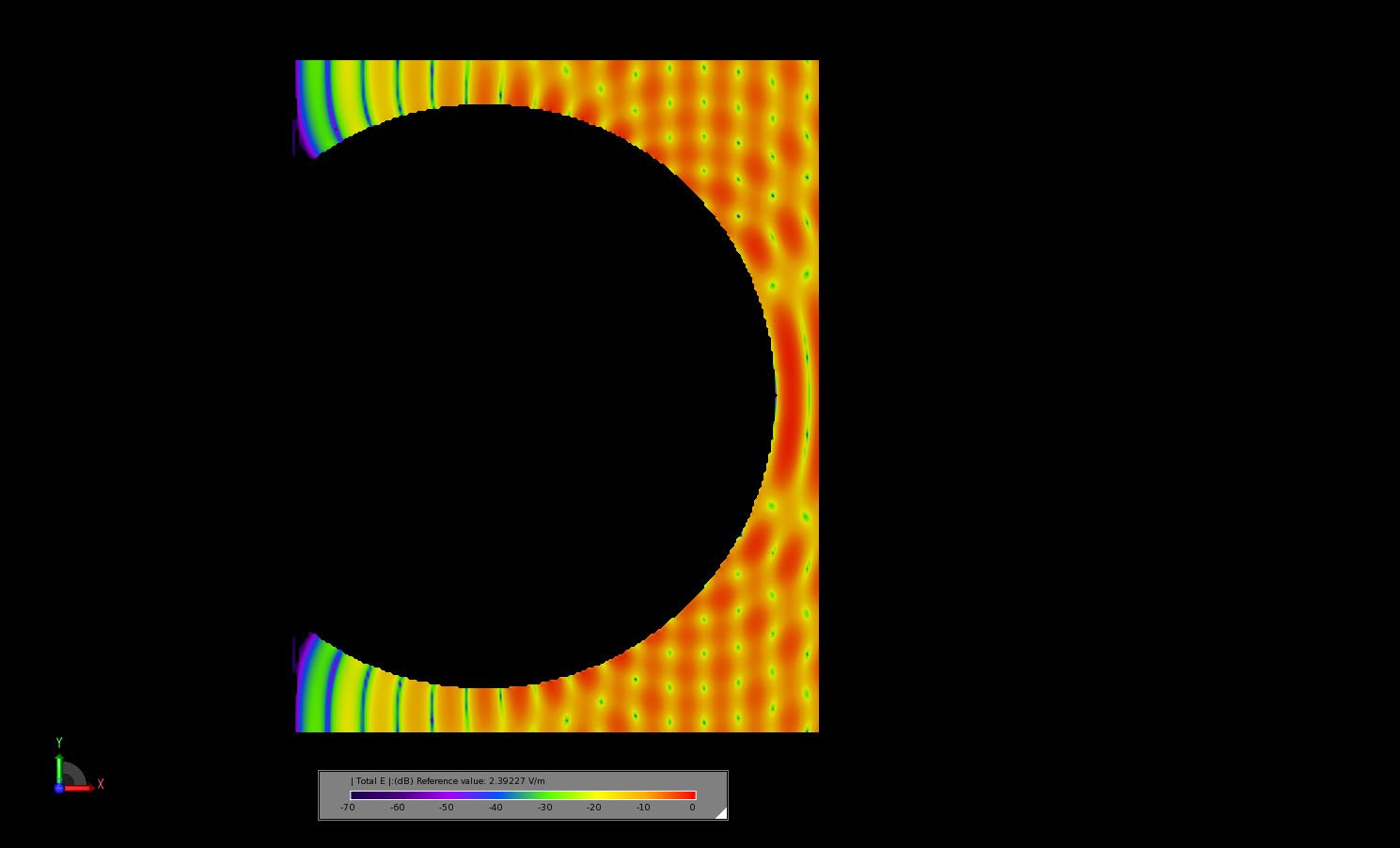
Figure 8: The transient electric field in a slice through the center of the sphere is shown at a time instance where the incident plane wave has struck the sphere and fields are propagating around the sphere surface.
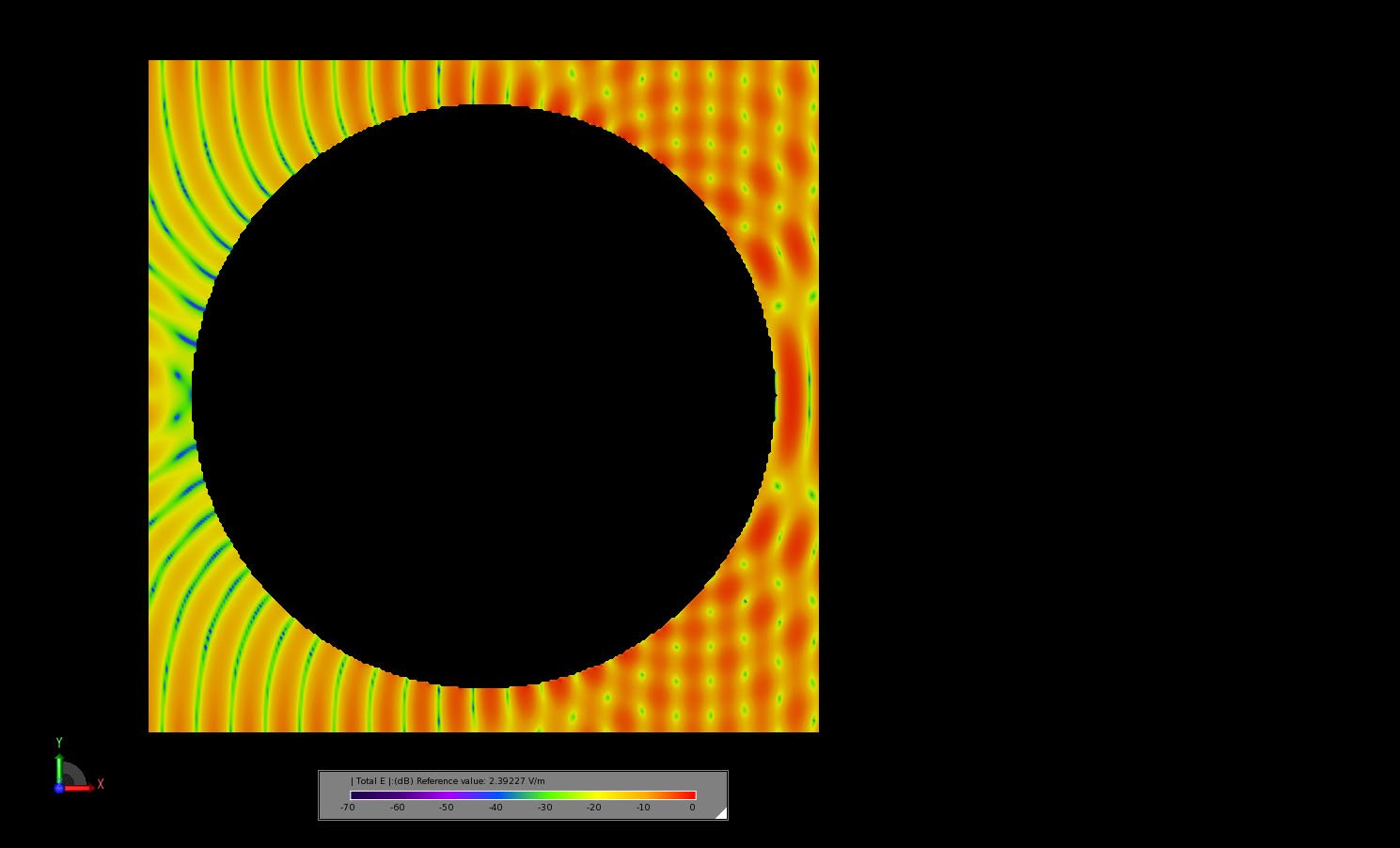
Figure 9: The transient electric field in a slice through the center of the sphere a time when the fields have reached steady-state.
References
-
R. A. Marr, U. H. W. Lammers, T. B. Hansen, T. J. Tanigawa, and R. V. McGahan, “Bistatic RCS Calculations From Cylindrical Near-Field Measurements—Part II: Experiments,” IEEE Trans. Antenna Propag., Vol. 54, Dec. 2006, pp. 3857-3863.
Request Project Files
Thank you for your interest in this application example. Please complete the form below to download the Conducting Sphere Bistatic Scattering project files.